Metropolis Algorithm for Expectations
The objective of this website is to prove the properties of the Metropolis algorithm with probability distribution \(\mu\); reversibility, irreducibility and aperiodicity. Furthermore we also extend the properties of the Metropolis algorithm with a probability distribution \(\mu = 1\)(no rejection) to the Travelling Salesperson Problem. The classic problem is to find the shortest possible Hamiltonian circuit, where a Hamiltonian circuit is defined as a sequence which starts at a predefined vertex, visits every other vertex in the state space once and returns to its start point. The application of the algorithm we explore is approximating the expected travel time of Hamiltonian circuits chosen uniformly with the added caveat of forbidden travel(i.e. sampling from a non-complete graph).
To put it in layman’s terms; a tourist wishes to leave his city to travel to 19 cities and then return home, and only wants to stay at each city once. Furthermore, a few cities do not directly link to one another directly. We aim to compute the average amount of time that it would take for our tourist to complete his trip, assuming that our tourist is whimsical and lets chance decide where his next destination is.
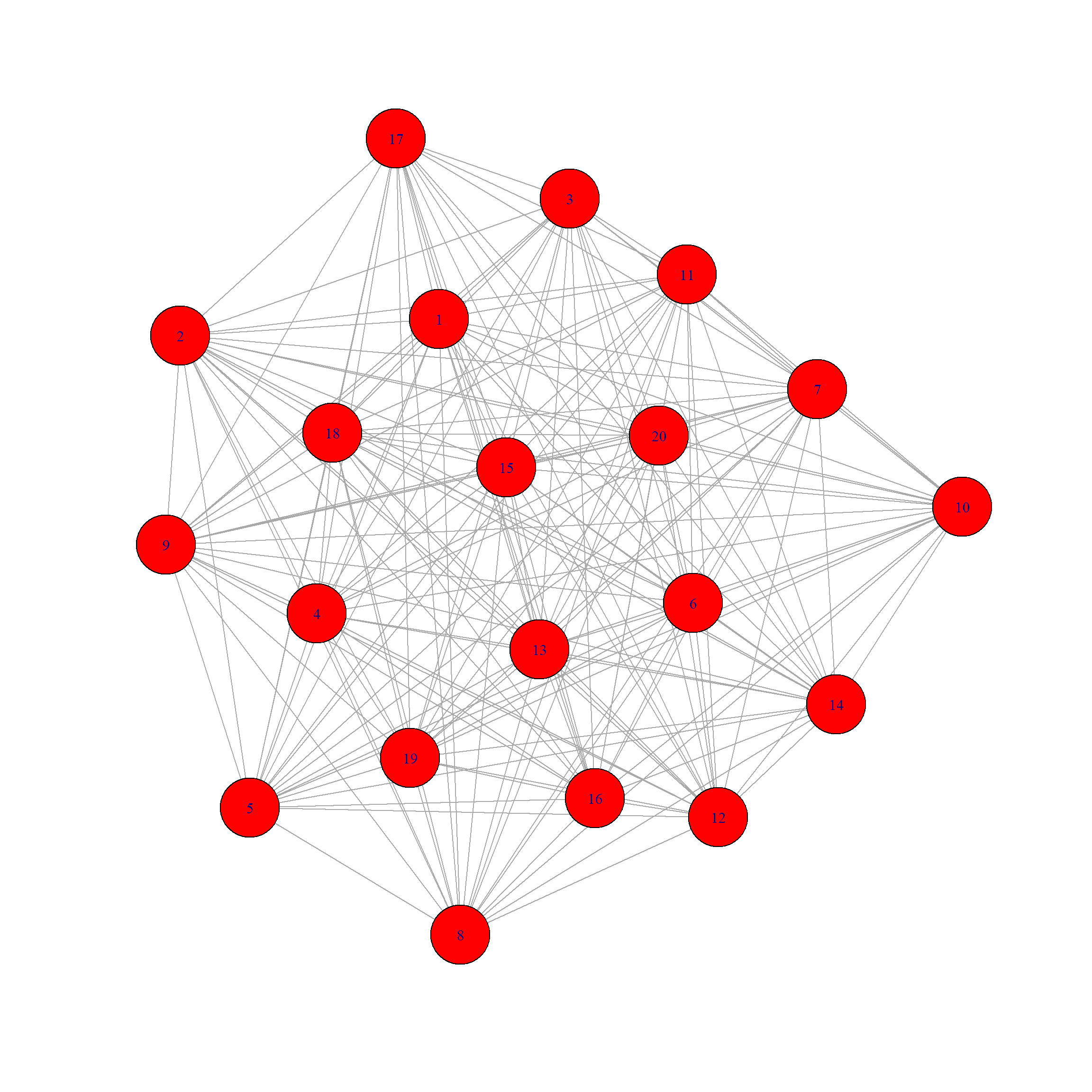
Non-complete graph with 20 vertices and 185 edges.